| 相関 |
| 相関とは |
|
相関関係
2変数データに関連性がある時(例えば,片方が大きいと,もう片方も大きくなるなど),その2つの変数には相関があるといいえる。
相関関係の種類
(1)正の相関
X、Yという2つの変数による散布図で、Xが増加するとYも増加する傾向にある場合。
(2)負の相関
Xが増加しているにもかかわらずYが減少する傾向にある場合。
(3)完全相関
相関係数が1叉は−1の場合。
(4)無相関
相関係数が0の場合。
相関関係と因果関係
相関関係は因果関係を含意しない。
すなわち、2つの変数の相関が自動的に一方がもう一方の原因を意味するというわけではない。
擬似相関
2つの事象に因果関係がないのに、見えない要因(潜伏変数)によって因果関係があるかのように推測されること。
擬似相関は2つの集団間に意味の有る関係があるような印象を与えるが、客観的に試験するとそれは無効である。
擬似相関は、第三の原因変数を導入することで生み出される。
|
| 相関分析と回帰分析 |
|
相関分析とは
2つ以上の変数がある場合に,それぞれの間に相関関係があるかどうかを検定すること。
2変数の間に線形関係があるかどうか、およびその強さについての分析であり、2つの変数の間に質的な区別を仮定しない。
回帰分析とは
変数の間にどのような関係があるか(具体的な関数の形)についての分析であり、また説明変数によって目的変数を予測するのを目的としている。
|
| 相関係数 |
| 相関係数 |
|
相関係数とは
2つのデータの間の関係の強さを測る統計量を相関係数 r という。
2組の数値からなるデータ列{(Xi,Yi)}(i=1,2,3・・・・) があたえられたとき、相関係数は以下のように求められる。
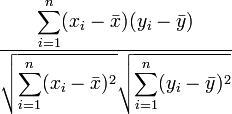
相関係数の見方
単位は無く、-1 から 1 の間の実数値をとり、1 に近いときは2 つの確率変数には正の相関があるといい、-1 に近ければ負の相関があるという。
0 に近いときはもとの確率変数の相関は弱い。
1もしくは -1 となる場合は 2 つの確率変数は線形従属の関係にある。
|
| 正の相関 |
相関の強さの判定 |
負の相関 |
| +1 〜 +0.7 |
強い相関がある |
−1 〜 −0.7 |
| 0.7 〜 0.4 |
中程度の相関がある |
−0.7 〜 −0.4 |
| 0.4 〜 0.2 |
弱い相関がある |
−0.4〜 −0.2 |
| 0.2 〜 0 |
ほとんど相関がない |
−0.2〜 0 |
|
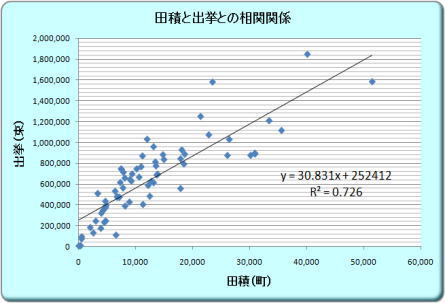 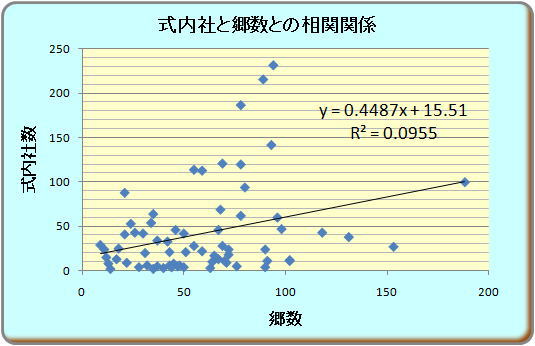 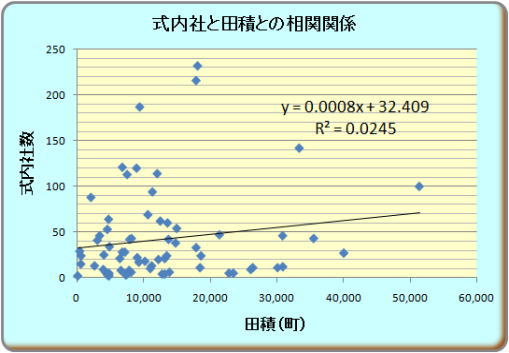 |
| r=0.82 r=0.31 r=0.16 |
説明率
rを2乗すると「説明率」になり、%として読むことができる。
例えば、相関係数が0.70であれば、説明率は0.702=0.49であり、一方の変数が他方の変数の49%の動きを説明することがわかる。
|
| 相関係数の種類 |
|
ピアソンの積率相関係数(Pearson product-moment correlation coefficient)
一般的な相関係数
これは偏差の正規分布を仮定する(パラメトリック)方法
スピアマンの順位相関係数
順位データから求められる相関の指標。
チャールズ・スピアマン(Charles Spearman)によって提唱され、ふつうρ と書かれる。
ピアソンの積率相関係数(普通に相関係数と呼ばれるもの)と違い、ノンパラメトリックな指標である。
すなわち2つの変数の分布について何も仮定せずに、変数の間の関係が任意の単調関数によってどの程度忠実に表現できるかを、評価するものである。
「変数間の関係は線形である」と仮定する必要も、また変数を数値的にとる必要もなく、順位が明らかであればよい。
原理的にはρ はピアソンの積率相関係数の特別な(相関係数を計算する前にデータを順位に変換した)場合に当たる。
|
| 相関係数の算出方法 |
|
1:散布図を書く
1) X軸(横軸)には原因となる変量を, Y 軸(縦軸)には結果となる変量をとる。
2:表計算ソフト(エクセル等)でrを算出する。
|
| 参考資料 |
|
「統計学要論」 (共立出版 1975)
「バイオサイエンスの統計学」 (南江堂 1994)
「医学・公衆衛生学のための統計学入門」 (南江堂 1988)
「図解 確率・統計の仕組みがわかる本」 (技術評論社 2008 長谷川勝也)
「Excelでここまでできる統計解析」 (日本規格協会 2007 今里健一郎 森田浩)
「エビデンス主義 統計数値から常識のウソを見抜く」 (角川SSコミュニケーションズ 2009 和田秀樹)
|
 |
「ファンタジ−米子・山陰の古代史」は、よなごキッズ.COMの姉妹サイトです |
  |
|