| 符号検定 |
| 概念 |
|
対応のある2変数の組について,母代表値に差があるか検定する。
符号検定では各ペアの差の符号(+or-)に注目して検定する。この+と-の数には有意に差があるといってよいかを調べる検定である。
2変数の組で単に,いずれが優れているか劣っているかあるいは同等であるかしかわからないときに適用する
(どの程度優れているか劣っているかが量的に定義できるときはウィルコクソンの符号付順位和検定を用いる)。
|
| 検定方法 |
|
(1)仮説の設定
帰無仮説 H0:2群間に差がない、と仮定する。
対立仮説 H1:2群間に差がある、と仮定する。
(2)統計量の計算
2群間に差がないならば、+と-の符号がでる確率は両方とも1/2である。
もし、2群間に差があるならば+と-の符号がでる確率はどちらかに偏るはずである。
符号検定では+と-の符号を見るので、各ペアの差が0のペアはデータから除外する。
また、符号の数が少ない方の個数をrとする。
帰無仮説が成立するならrが出現する確率は1/2であり、二項分布に従うことになる。
この計算によってr値がその値以上の極端な値をとる確率を求める。
(3)確率の計算・判定
小標本の場合(5<n≦25の時)
直接計算して確率を求めればよい。
大標本の場合(n>25の時)
下の式より平均値と標準偏差を出して、その後z値をだす。
z値を求めたら標準正規分布表から確率Pを求める。

(4)判定
P≧αのとき、帰無仮説を棄却できない。
P<αのとき、帰無仮説を棄却する。有意差あり。
|
| χ2(カイ二乗)検定 |
| χ2検定の概念 |
| χ2検定とは |
|
カイ二乗検定
帰無仮説が正しければ検定統計量がカイ二乗分布に従うような統計学的検定法の総称である。
次のようなものが含まれる。
ピアソンのカイ二乗検定: カイ二乗検定として最もよく利用されるものである(通常はこれを指す)。
一部の尤度比検定: 標本サイズが大きい場合には近似的にカイ二乗検定となる場合がある。
イェイツのカイ二乗検定(イェイツの修正)
マンテル・ヘンツェルのカイ二乗検定
累積カイ二乗検定
Linear-by-linear連関カイ二乗検定
|
| ピアソンのカイ二乗検定 |
|
カイ二乗検定のうち最も基本的かつ広く用いられる方法であって、「観察された事象の相対的頻度がある頻度分布に従う」という帰無仮説を検定するものである。
カイ二乗は各頻度の観測値と理論値の差を2乗し、各頻度の理論値で割って、合計したものである。
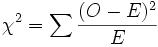
ただしここでO = 頻度の観測値、E = 帰無仮説から導かれる頻度の期待値(理論値)である。ピアソンのカイ二乗検定は2つのタイプの比較、適合度検定および独立性検定に用いられる
|
| X2適合度検定 |
| 概念 |
|
目的
X2適合度検定はデータが予測される確率(割合)の通りになっているかどうかを判定する。
観測度数(Ok)は実際に行って観測した数値、期待度数(Ek)は予測される数値。
よって、両群の差を検定することになる。
例
サイコロを振って1の目が出る確率は普通1/6である。しかし、サイコロに細工をすればそうはいかない。このようなサイコロの目の出方が一様であるかどうかを調べるには、X2適合度検定を使う。 |
| 分類 |
A1 |
A2 |
… |
Ak |
| 観測度数 |
O1 |
O2 |
… |
Ok |
| 期待度数 |
E2 |
E2 |
… |
Ek |
|
|
| 検定方法 |
|
(1)仮説の設定
帰無仮説 H0:観測度数と期待度数の数値は一致する、と仮定する。
対立仮説 H1:観測度数と期待度数には有意に差がある、と仮定する。
(2)統計量の計算
観測度数Oと期待度数Eとのずれは次の式によって定量化することができる。
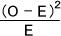
全体の偏りは、次の式によって表せる。
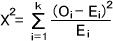
観測度数Oiと期待度数Eiの全体のずれが偶然起こったものであるなら、ここで求めたX2値はX2に従う。
ただし自由度dfは理論度数によって異なり、下のようになる。
一様分布のとき、df=k-1
二項orポアソン分布のとき、df=k-2
正規分布のとき、df=k-3
このときのkは分類した数である。また一様分布とは、全ての区間を同等の値をとる分布である。
(3)確率の計算
自由度を求めたらX2分布表からX2αを出す。
(4)判定
X2≦X2αのとき、P≧αとなり帰無仮説を棄却できない。
X2>X2αのとき、P<αとなり帰無仮説を棄却する。有意差あり。
|
| X2独立性検定 |
| 概念 |
|
目的
2つの変数に対する2つの観察(2x2分割表で表される)が互いに独立かどうかを検定する。
例
「別の地域の人々について、選挙である候補を支持する頻度が違う」かどうかを検定。
補足
X2適合検定ではひと続きの独立なデータとして分類した。
それに対し、2×2分割表は行・列がそれぞれ二方向ある分類である。
X2適合検定で観測度数と期待度数の偏りを計算してX2値を求めたのと同じように、2×2分割表の計算でも観測度数と期待度数の偏りを計算してX2値を求める。2×2分割表では行・列での値が互いに独立かどうかを検定する。 |
| 分類 |
A1 |
A2 |
… |
Ak |
| 観測度数 |
O1 |
O2 |
… |
Ok |
| 期待度数 |
E2 |
E2 |
… |
Ek |
↑X2適合検定 |
|
|
B1 |
B2 |
合計 |
| A1 |
a |
b |
R1 |
| A2 |
c |
d |
R2 |
| 合計 |
C1 |
C2 |
N |
↑2×2分割表 |
|
| 検定方法 |
|
(1)仮説の設定
帰無仮説 H0:行・列の度数配置に差がない、と仮定する。
対立仮説 H1:行・列の度数配置に差がある、と仮定する。
(2)統計量・確率の計算
2×2分割表では、期待度数と観測度数の偏りを下の式によって表すことができる。
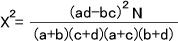
2×2分割表は自由度1のX2分布に従うので、X2分布表より自由度1のX2αを求める。
(3)判定
X2≦X2αのとき、P≧αとなり帰無仮説を棄却できない。
X2>X2αのとき、P<αとなり帰無仮説を棄却する。有意差あり。
|
| 参考資料 |
|
「統計学要論」 (共立出版 1975)
「バイオサイエンスの統計学」 (南江堂 1994)
「医学・公衆衛生学のための統計学入門」 (南江堂 1988)
「図解 確率・統計の仕組みがわかる本」 (技術評論社 2008 長谷川勝也)
「Excelでここまでできる統計解析」 (日本規格協会 2007 今里健一郎 森田浩) |
|
 |
「ファンタジ−米子・山陰の古代史」は、よなごキッズ.COMの姉妹サイトです |
  |
|