| ウィルコクソンの符号付順位和検定 (signed rank test) |
| 概念 |
|
目的
対応のある2変数の組について、代表値に差があるか否かを検定する。
ウィルコクソンの符号付順位和検定では、2変数のとる値の差が定義でき,かつ,差の順位付けができなければならない。
この条件が満たされないときには符号検定を用いること。
順序尺度・順序分類尺度 関連2群・・・・代表値の検定
|
| 検定方法 |
|
(1)仮説の設定
前提帰無仮説 H0:母代表値に差はない。
対立仮説 H1:母代表値に差がある。
(2)統計量の計算
有意水準 α で両側検定を行う(片側検定も定義できる)。
n ケースの、対応のある 2 変数を Xi,Yi,両者の差を di =
Xi - Yi とする(i = 1,2,... ,n)。
Xi - Yi の絶対値の小さい方から順位をつける。ただし,Xi=Yi
の組は除く。
同順位の場合は平均順位をつける。
Xi > Yi の組の順位の和と Xi < Yi
の組の順位の和のうち,小さい方を検定統計量 T とする。
(3)確率の計算・判定
Xi ≠ Yi の組の数 N が小さいとき
統計数値表を参照して棄却限界値を求める。
N ≦ 50 ならば,ウィルコクソンの符号付順位和検定統計量の分布を参照することにより、正確な有意確率を求めることができる。
帰無仮説の採否を決める。
検定統計量 > 棄却限界値ならば、帰無仮説を採択する。→「母代表値に差があるとはいえない」。
検定統計量 ≦ 棄却限界値ならば、帰無仮説を棄却する。→「母代表値に差がある」。
Xi ≠ Yi の組の数 N が大きいとき(正規分布による近似)
次式で検定統計量を計算する。Z0 は、正規分布に従う。
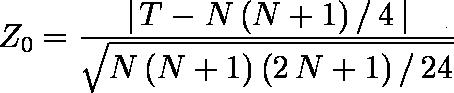
有意確率を P = Pr{| Z | ≧ Z0} とする。
正規分布表,または正規分布の上側確率の計算を参照すること。
帰無仮説の採否を決める。
P > α のとき,帰無仮説を採択する。「母代表値に差があるとはいえない」。
P ≦ α のとき,帰無仮説を棄却する。「母代表値に差がある」。
|
| ウィルコクソンの順位和検定 (Wilcoxon rank sum test) |
| 概念 |
|
目的
t検定に対応し、t検定で必要とされる仮定が満たされない場合に用いる。
順序尺度・順序分類尺度 独立2群・・・・代表値の検定
|
| 検定方法 |
|
(1)仮説の設定
全2n 回の観察で、n 個の対象に対し各2回の観察を行うとする。
i で各対象を表し、i
に対する1回目の測定値を xi 、2回目の測定値を
yi とする。
次のように仮定する。
i =1,・・・,nに対し Zi = Yi −
Xi とする。
各差 Zi は互いに独立とする。
各Zi は連続的母集団(同じでなくてよい)に由来し、共通の中央値θ
に関して対称とする。
帰無仮説H0 をθ = 0 とする。
(2)統計量の計算
絶対値| Z1 |、・・・・、| Zn|を順番に並べ、各 | Zi | の順位をRi として、これからウィルコクソンの符号順位統計量W + を計算する。
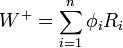
φi = I(Zi >
0) (ただしI(.) は指示関数、すなわちZi > 0のとき I(Zi) = 1、Zi = < 0のとき I(Zi) = 0)とする。
(3)確率の計算と判定
前後2回データを収集した場合の点数(中心点が0と期待される)の差を検定するのによく用いられる。
中心点と完全に一致する点数は除外し、残りの点数の中心点からの偏差の絶対値を順位化し、最小の偏差が順位1となるようにする。
タイ(同順位)点数には平均順位を充てる。中心点からの正・負の両偏差ごとに順位の和を計算する。両順位和の小さい方をS とする。
そしてS を順位分布の数表と比較してp値(中心点の周りに対称に分布する点数母集団から、その値以上のS 値が得られる確率)を求める。
|
| マン・ホイットニー(Mann-Whitney)のU検定 |
| 概念 |
|
概念
独立した2群間の比較出用いるノンパラメトリックな検定。
ウィルコクソンの順位和検定と実質的に同じ方法であり、まとめてマン・ホイットニー・ウィルコクソン検定とも呼ばれる。
ウィルコクソンの順位和検定 (Wilcoxon rank sum test) を用いるとの記載もあるが、結果は同じになる。
順序尺度・順序分類尺度 独立2群・・・・代表値の検定
目的
独立な2組の標本の有意差検定として用いられる。
変数は順位としてとれば(つまり2つを比較してどちらが大きいかがわかっていれば)よい。
2つの観察された分布の間の重なりの度合が偶然で期待されるよりも小さいかどうかを、「両標本が同じ母集団から抽出された」との帰無仮説に基づいて検定する方法である。
U (帰無仮説の下ではその分布がわかっている)と呼ばれる統計量を求める。
標本サイズが小さい場合にはこの分布は数表になっている。
約20以上の場合には正規分布でよい近似ができる。
|
| 検定の前に |
|
小標本に対して(n≦20)
直接計算する。
簡単にできて統計量U の意味が理解しやすい。
観察度数あるいは標本サイズが小さいほうの標本を選んで、これを標本1、もう一方を標本2とする。
標本1の各観察について、標本2の中でそれよりも小さい値が得られた観察の度数を数える。これらの度数をすべて総和したものがU
である。
大標本に対して(n>20)
公式を用いる。
すべての観察を並べて1つの順位系列とし、小さい方の標本の順位を総和する。全ての順位の和はN(N
+ 1)/2 (ここで N は全観察数)に等しいから、U は次のように求められる
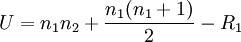
ここで n1 と n2 は2組の標本の大きさで、
R1 は標本1.の順位の和である。
U
の最大値は2標本の大きさの積で、上記の方法で得られた値がこの最大値の半分より大きい場合は、それを最大値から引いた値を数表で見つけ出せばよい。
|
| 検定方法 |
|
(1)仮説の設定
帰無仮説(H0):μA=μB
対立仮説(H1):μA≠μB.................(両側検定のとき)
対立仮説(H1):μA>μB, または
μA<μB(片側検定のとき)
(2)統計量Uの計算
危険率(100α%)を設定する。(両側検定の有意水準:α/2 片側検定の有意水準:α)
各群のデータ数をn1、n2 とし、総データ数をn とする。
2つの群のデータすべてを小さい順に並べ、小さいほうから順位をつける。
同順位がある場合は、平均順位をつける。
各群につけられた順位の和R1、R2 を求める。
検定量U1、U2 を求める。
U1 = n1 ×n2 + n1 ×(n1 +1) / 2-R1 U2 = n1× n2 + n2× (n2+1) / 2-R2
検定統計量は、U1, U2 のいずれか小さいほう U0 = min(U1, U2) とする。
(3)確率の計算・判定
小標本の場合(各群のデータ数をn1、n2 が何れも20 以下の時)
統計表の値とMann-Whitney検定表を比較し、計算値U0 のほうが小さい時に、帰無仮説を棄却する。
大標本の場合(各群のデータ数をn1、n2 の大きいほうが20 を超えている時)
U1、U2 の分布は正規分布に近似していることが知られているので、次式により標準化を行い、正規分布表から確率を求める。
Z0=(U0-n1n2/2)/〔[n1n2(n1+n2+1)]/12〕1/2
Z0 の値より得られた表の値を2 倍したものが、有意確率P となる。
P > α のとき,帰無仮説を採択する。(α は、危険率0.05)
P ≦ α のとき,帰無仮説を棄却する。
|
| 参考資料 |
|
「統計学要論」 (共立出版 1975)
「バイオサイエンスの統計学」 (南江堂 1994)
「医学・公衆衛生学のための統計学入門」 (南江堂 1988)
「図解 確率・統計の仕組みがわかる本」 (技術評論社 2008 長谷川勝也)
「Excelでここまでできる統計解析」 (日本規格協会 2007 今里健一郎 森田浩) |
|
 |
「ファンタジ-米子・山陰の古代史」は、よなごキッズ.COMの姉妹サイトです |
  |
|